%pylab inline
Populating the interactive namespace from numpy and matplotlib
font = {'size': 16}
matplotlib.rc('font', **font)
In this document we will describe the difference between convex/concave, and show how to test if a function is convex/concave for single and multivariable functions.
Convex¶
A real-valued function on an n-dimensional interval is called convex (or convex downward or concave upward) if the line segment between any two points on the graph of the function lies above or on the graph, in a Euclidean space (or more generally a vector space) of at least two dimensions.
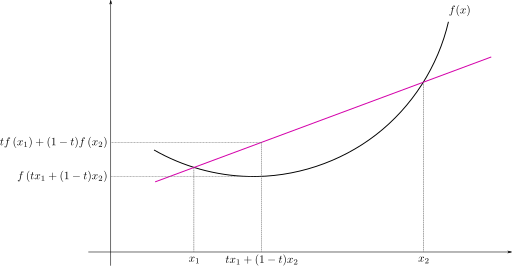
Convex functions play an important role in many areas of mathematics. They are especially important in the study of optimization problems where they are distinguished by a number of convenient properties. For instance, a (strictly) convex function on an open set has no more than one minimum. Even in infinite-dimensioinal space, under suitable additional hypotheses, convex functions continue to satisfy such properties.
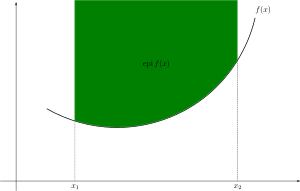
A function (in black) is convex if and only if the region above its graph (in green) is a convex set. A convex set is a collection of points such that, for each pair of points in the collection, the entire line segment joining these two points is also in the collection.
Concave¶
A set that is not convex is a called a non-convex set. A polygon that is not a convex polygon is sometimes called a concave polygon, and some sources more generally use the term concave set to mean a non-convex set, but most authorities prohibit this usage.
The complement of a convex set, such as the epigraph of a concave function, is sometimes called a reverse convex set, expecially in the context of mathematical optimization.
Single variable convexity/concavity test¶
Let $f$ be any single variable function. We can test if $f$ is concave/convex by finding the second derivative of $f$, and testing the following three cases:
- $f''(x) > 0 \rightarrow f$ is convex at $x$.
- $f''(x) < 0 \rightarrow f$ is concave at $x$.
- $f''(x) = 0 \rightarrow f$ has an inflection point at $x$.
The inflection point determines when the function convexity/concavity of $f$ changes.
Example¶
Let $f(x)=5x^3 + 4x^2 + 6x$. If we differentiate $f$, we get $f'(x)=15x^2+8x+6$. Differentiating again, for the second derivative, we get $f''(x)=30x+8$. If we plot $f(x)$ and $f''(x)$, we get:
X = np.linspace(-10, 10, 40) # x
Y1 = [(lambda x: 5*x**3 + 4*x**2 + 6*x)(x) for x in X] # f(x)
Y2 = [(lambda x: 30*x + 8)(x) for x in X] # f''(x)
plot(X,Y1,c='b',lw=2)
plot(X,Y2,c='r',lw=2,ls='dashed')
grid();xlabel('$x$');ylabel('$f(x)$ and $f\'\'(x)$')
title('Graph of $f(x)$ and $f\'\'(x)$');
We know the inflection point is where $f''(x)=0$, therefore $30x+8=0$, which means that the inflection point is at $x=-\frac{8}{30}$.
Now we will test if the second derivative is positive/negative on each side of the inflection point:
- $f''(-5) = -142 \rightarrow f$ is concave at $x=-5$.
- $f''(5) = 156 \rightarrow f$ is convex at $x=5$.
Because we know the inflection point, we now know that $f$ is convex on the interval $\left[-\frac{8}{30}, \rightarrow\right>$. In a similar way, we also know that $f$ is concave on the interval $\left<\leftarrow, -\frac{8}{30}\right]$.
Two variable convexity/concavity test¶
We can also test for convexity/concavity for two variable functions. If we look at an example function $f(x,y)=x^2+xy+y^2$, we can clearly see that it is strictly convex.
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(14,10))
ax = fig.add_subplot(111, projection='3d')
xs = ys = np.arange(-5, 5, .05)
X, Y = np.meshgrid(xs, ys)
zs = np.array([(lambda x, y: x**2 + x*y + y**2)(x, y) for x, y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)
surf = ax.plot_surface(X, Y, Z, cmap=cm.jet)
fig.colorbar(surf, shrink=0.5, aspect=5)
xlabel('X');ylabel('Y');ax.set_zlabel('$f(x,y)$')
title('Surface plot of $f(x,y)=x^2+xy+y^2$');
Method for functions of two variables¶
To determine if $f(x,y)$ is concave or convex, we need to find the following four quantities:
- $\dfrac{\partial^2 f(x,y)}{\partial x^2}$ : The second partial derivative of $f(x,y)$ with respect to $x$.
- $\dfrac{\partial^2 f(x,y)}{\partial y^2}$ : The second partial derivative of $f(x,y)$ with respect to $y$.
- $\dfrac{\partial^2 f(x,y)}{\partial x \partial y}$ : The first partial with respect to $x$, and the second partial with respect to $y$.
- $\dfrac{\partial^2 f(x,y)}{\partial y \partial x}$ : The first partial with respect to $y$, and the second partial with respect to $x$.
It is important to note that if we first take the partial with respect to $x$ and then with respect to $y$, we will get the same as if we first take it with respect to $y$ and the with respect to $x$. This means that $\dfrac{\partial^2 f(x,y)}{\partial x \partial y}$ is the same as $\dfrac{\partial^2 f(x,y)}{\partial y \partial x}$. Therefore it is sufficient to find one of them, and squaring them to get $\left[\dfrac{\partial^2 f(x,y)}{\partial x \partial y}\right]^2$.
After we have found the quantities, we can compare them in the following table to see if $f(x,y)$ is convex/concave, or none at all:
| Quantity | Convex | Strictly convex | Concave | Strictly concave |
|---|---|---|---|---|
| $\dfrac{\partial^2 f(x,y)}{\partial x^2} \cdot \dfrac{\partial^2 f(x,y)}{\partial y^2} - \left[ \dfrac{\partial^2 f(x,y)}{\partial x \partial y} \right]^2$ | $\geq 0$ | $>0$ | $\geq 0$ | $> 0$ |
| $\dfrac{\partial^2 f(x,y)}{\partial x^2}$ | $\geq 0$ | $>0$ | $\leq 0$ | $< 0$ |
| $\dfrac{\partial^2 f(x,y)}{\partial y^2}$ | $\geq 0$ | $>0$ | $\leq 0$ | $< 0$ |
A quick way to determine if a function is convex or concave, is by finding the quantities in the following matrix:
$$ M = \begin{bmatrix} \dfrac{\partial^2 f(x,y)}{\partial x^2} & \dfrac{\partial^2 f(x,y)}{\partial x \partial y} \\ \dfrac{\partial^2 f(x,y)}{\partial y^2} & \dfrac{\partial^2 f(x,y)}{\partial y \partial x} \end{bmatrix} $$
If $f(x,y)$ is convex/concave, this means that $\textrm{det}(M) \geq 0$. If we remember that $\text{det}(M) = ad-bc$, we can see that the $\textrm{det}(M)$ becomes:
$$ \dfrac{\partial^2 f(x,y)}{\partial x^2} \cdot \dfrac{\partial^2 f(x,y)}{\partial y^2} - \dfrac{\partial^2 f(x,y)}{\partial x \partial y} \cdot \dfrac{\partial^2 f(x,y)}{\partial y \partial x} \geq 0 $$
But if we recall that $\dfrac{\partial^2 f(x,y)}{\partial x \partial y}$ is the same as $\dfrac{\partial^2 f(x,y)}{\partial y \partial x}$, we can rewrite it as:
$$ \dfrac{\partial^2 f(x,y)}{\partial x^2} \cdot \dfrac{\partial^2 f(x,y)}{\partial y^2} - \left[\dfrac{\partial^2 f(x,y)}{\partial x \partial y}\right]^2 \geq 0,$$
which is the quantity in the table.
Example¶
Let $f(x,y)=x^2+xy+y^2$. We first determine the four quantities:
- $\dfrac{\partial^2 f(x,y)}{\partial x^2} = 2$.
- $\dfrac{\partial^2 f(x,y)}{\partial y^2} = 2$.
- $\dfrac{\partial^2 f(x,y)}{\partial x \partial y} = 1$.
- $\dfrac{\partial^2 f(x,y)}{\partial y \partial x} = 1$.
If we let $M=\begin{bmatrix} 2 && 1 \\ 1 && 2 \end{bmatrix}$ we find that $\textrm{det}(M)=2\cdot2-1\cdot1 = 4-1 = 3$. This means that the function is either convex or concave.
If we look at the table we can see that $\dfrac{\partial^2 f(x,y)}{\partial x^2} > 0$ and $\dfrac{\partial^2 f(x,y)}{\partial y^2} > 0$. This means that $f(x,y)$ is a strictly convex function.
References¶
- https://en.wikipedia.org/wiki/Convex_set
- https://en.wikipedia.org/wiki/Convex_function
- Introduction to Operations Research, Hillier/Lieberman, chapter 13.