Rendering
Camera
This is used to create an orthonormal basis for the camera. This can then be used to easily navigate the camera, because we have vectors to go forward, left, or up (and the inverse of those).
1 2 3 4 5 6 | |
- \(\textrm{ro}\) is the ray origin.
- \(\textrm{ta}\) is the target (where we are looking at).
- \(\textrm{ww}\), \(\textrm{uu}\), \(\textrm{vv}\) is the orthonormal basis.
- \(\textrm{rd}\) is the ray direction.
Raymarcher
Description
A raymarching algorithm will intersect the scene by stepping a ray into the scene. At each step the distance, \(d\), to the nearest object is calculated with a signed distance function, which is then used as the distance to safely step forward. An object is hit when the distance is smaller than some \(\epsilon\), for example: \(d < 0.001\). This illustration visualizes this process.
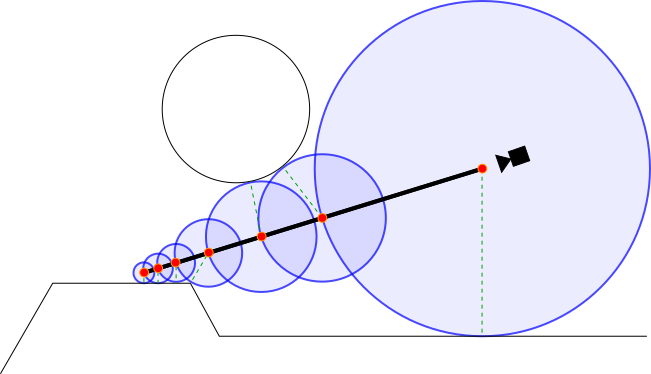
The algorithm requires a ray origin ro, and a ray direction rd as input.
The output of the algorithm is a value t, which is the distance from the origin to the intersection point.
This intersection point \(P\) is then calculated with \(P = \textrm{ro} + t\cdot \textrm{rd}.\)
The algorithm has the following global parameters:
| Variable | Description |
|---|---|
MIN_MARCH_DISTANCE |
The minimum distance to the object to qualify as a hit. Lower values will increase the detail, but slow down the algorithm. |
MAX_MARCH_DISTANCE |
The maximum distance that a ray is allowed to travel. Larger values will render the scene further, but slow down the algorithm. |
MAX_MARCH_STEP |
The maximum amount of steps the algorithm is allowed to take. Increase this if the detail between complex objects is poor. Higher values will slow down the algorithm. |
Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | |
Info
The algorithm requires a map(vec3 point) function (line 9), which is the output of a 3D SDF, for example:
1 2 3 | |
Normals
A normal vector is the vector \(\nabla f(\mathbf{X})\). This can be calculated numerically with the central differences method.
1 2 3 4 5 6 7 | |