Skip to content

Lighting models

All the lighting models described on this page use the following notation, as illustrated in the image below.

Source — Wikipedia

Let \(\mathbf{P}\) be the point on the surface, then:

  • \(\mathbf{N}\) is the normal vector of the surface at \(\mathbf{P}\).
  • \(\mathbf{L}\) is the vector from \(\mathbf{P}\) to the light source.
  • \(\mathbf{V}\) is the vector from \(\mathbf{P}\) to the camera (eye).
  • \(\mathbf{H}\) is the halfway vector between \(\mathbf{L}\) and \(\mathbf{V}\).
  • \(\mathbf{R}\) is the reflected vector \(\mathbf{V}\) around \(\mathbf{N}\).

To find the reflection vector, we can use \(\mathbf{R} = \mathbf{V} - 2(\mathbf{V}\cdot\mathbf{N})\mathbf{N}\), where \(\mathbf{V}\cdot\mathbf{N}\) is a dot-product.

To find the halfway vector, we can use \(\mathbf{H} = \dfrac{\mathbf{L}+\mathbf{V}}{||\ \mathbf{L}+\mathbf{V}\ ||}\).

Attention

Note that all of these vectors must be normalized, which is often denoted with a hat, like \(\mathbf{\hat{N}}\).

Lambertian

Lambertian reflectance looks like an ideal "matte" or diffuse reflecting material. It is based on the angle between the light \(\mathbf{L}\) and the surface normal \(\mathbf{N}\):

\[ I_D = \mathbf{L}\cdot\mathbf{N}CI_L \]

where 

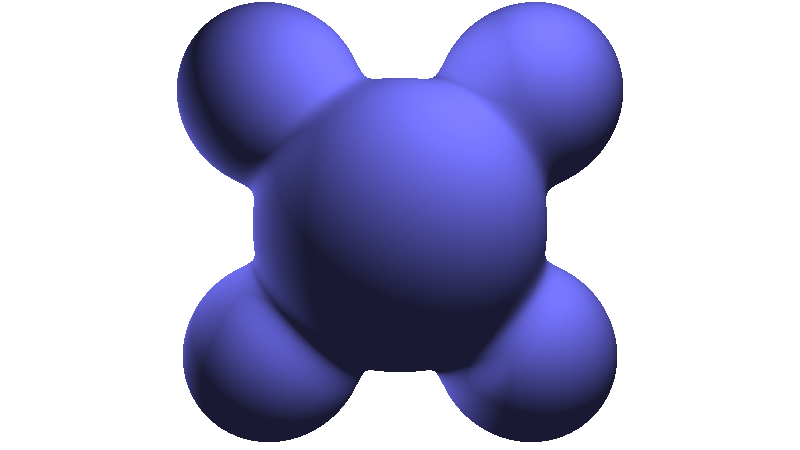
1
2
3
4
float brdf_lambertian(vec3 N, vec3 L) {
    float k = clamp(dot(N, L), 0., 1.);
    return k;
}

Lambertian (wrapped)

Wrapping the light can be used to fake subsurface scattering or area light. A parameter wrap is used which is a value between \([0, 1]\).

1
2
3
4
5
float brdf_lambertian_wrapped(vec3 N, vec3 L) {
    float wrap = 0.5;
    float k = max(0., (dot(L, N) + wrap) / (1. + wrap));
    return k;
}

Phong

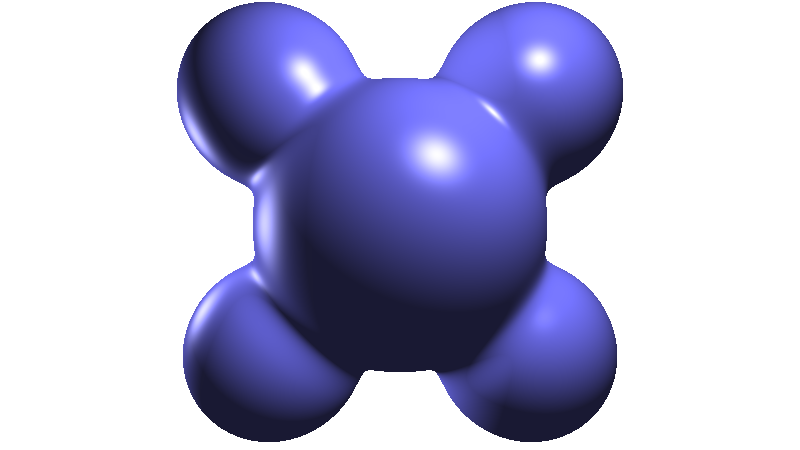
1
2
3
4
float brdf_phong(vec3 R, vec3 V, float exponent) {
    float k = pow(max(0., dot(R,V)), exponent);
    return k;
}

Blinn-Phong

TBA

Gaussian

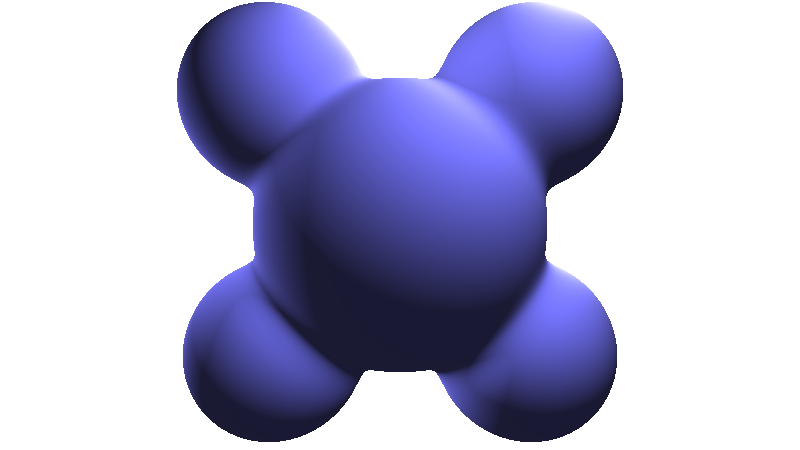
1
2
3
4
5
6
float brdf_gaussian(vec3 N, vec3 H, float m) {
    float NHm = angle(N,H) / m;
    float NHm2 = NHm*NHm;
    float k = exp(-NHm2);
    return k;
}

Beckmann

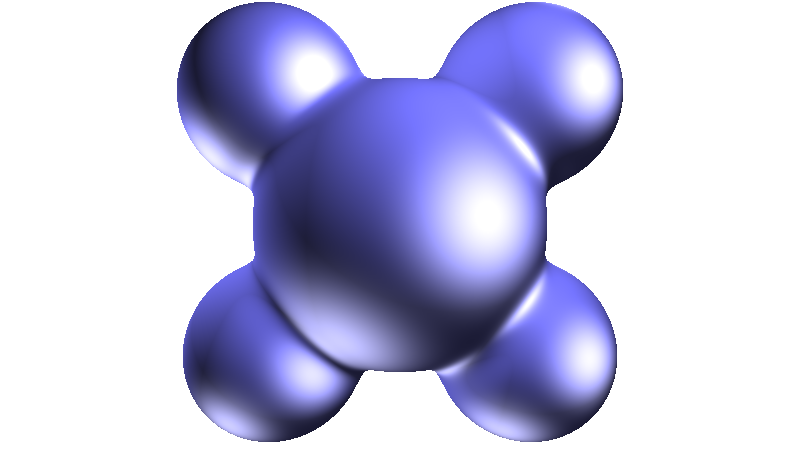
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
float brdf_beckmann(vec3 N, vec3 H, float m) {
    float NdotH = dot(N, H);
    float tana = length(cross(N, H)) / NdotH;
    float cosa = NdotH;
    float m2 = m*m;
    float tana2 = tana*tana;
    float cosa4 = pow(abs(cosa), 4.);
    float k = exp(-tana2 / m2) / (3.14159 * m2 * cosa4);
    return k;
}

GGX

The GGX lighting model is a microfacet model for refracting through rough surfaces. It is also a model that is becoming popular for lighting in video games. [1] The GGX lighting model is derived in this paper.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
float G1V(float dotNV, float k) {
    return 1.0 / (dotNV * (1.0 - k) + k);
}

float brdf_ggx(vec3 N, vec3 V, vec3 L, float roughness, float F0) {
    float alpha = roughness * roughness;
    vec3 H = normalize(V+L);
    float dotNL = clamp(dot(N,L), 0., 1.);
    float dotNV = clamp(dot(N,V), 0., 1.);
    float dotNH = clamp(dot(N,H), 0., 1.);
    float dotLH = clamp(dot(L,H), 0., 1.);
    float alphaSqr = alpha*alpha;
    float pi = 3.14159;
    float denom = dotNH * dotNH * (alphaSqr - 1.0) + 1.0;
    float D = alphaSqr / (pi * denom * denom);
    float dotLH5 = pow(1.0 - dotLH, 5.0);
    float F = F0 + (1.0 - F0) * dotLH5;
    float k = alpha / 2.0;
    float vis = G1V(dotNL, k) * G1V(dotNV, k);
    return dotNL * D * F * vis;
}

Author: John Hable

Further Reading

References